Sohrab Akhoundzadeh
Voorkomen is beter dan genezen. Dat geldt ook voor aardbevingen. Keer op keer zijn duizenden doden slachtoffer van verwoestende aardbevingen. Kinderen die onder het puin komen te liggen, families die in één klap wegvagen, mensen die opeens zonder onderdak
op straat belanden. Eén ding is zeker, de natuur is de natuur en heeft geen medelijden met het leven op aarde. Al jaren zijn seismologen bezig met het bedenken van methodes om te bepalen waar, wanneer en hoe aardbevingen zullen ontstaan.
Dit is tot vandaag de dag echter nog niet mogelijk, wegens de complexiteit, variabiliteit in seismische activiteit en de beperkte technologie. Hoewel het voorspellen van aardbeving nog niet mogelijk is, kan er wel worden gekeken naar
de waarschijnlijkheid van een mogelijke aardbeving dankzij moderne analysetechnieken. Hierbij wordt gebruik gemaakt van statistische modellen die rekening houden met de seismische activiteit en de historische data. Hiermee kunnen er
tegenwoordig benaderingen worden gemaakt over de waarschijnlijkheid van toekomstige aardbevingen.
Om de waarschijnlijkheid voor het optreden van een aardbeving te berekenen, moet er worden gekeken over een lange periode en moeten daaruit gegevens over het totaal aantal aardbevingen per jaar met een magnitude M of groter worden gekeken. De Heer Gutenberg
en Richter hebben in 1944 voor het eerst een wet gevonden, de Gutenberg-Richter wet, die het verband tussen het totaal aantal aardbevingen per jaar met een magnitude M kan uitdrukken:
log10(N) = a - bM 1
N = 10a - bM
In deze formule is N de totale hoeveelheid aardbevingen per jaar met een magnitude groter dan 0 en zijn a en b constante waarden.
Vervolgens wordt er ook nog gekeken naar de herhaalperiode T van een aardbeving. De herhaalperiode zegt iets over de gemiddelde tijd tussen het plaatsvinden van aardbevingen van een bepaalde magnitude in een specifieke locatie. Deze waarde is belangrijk
voor het berekenen van de waarschijnlijkheid van een aardbeving van deze magnitude of hoger. De herhaalperiode is vaak te halen uit geologische gegevens die de seismische activiteiten in bepaalde locaties per jaar hebben vastgesteld.
Het verband tussen de waarschijnlijkheid, terugkeerperiode en de hoeveelheid verstrijken tijd tussen de laatste en eerstvolgende aardbeving van magnitude M en hoger wordt gegeven door:
P = 1 - ( 1 -
)L 2
1
T
Hierbij is P de waarschijnlijkheid voor het optreden van een aardbeving met magnitude M of groter, T de herhaalperiode van deze aardbeving en L de verstrijken tijd tussen de laatste en meest recente aardbeving van deze magnitude. In het voorbeeld hieronder
is te zien hoe er verschuivingen plaatsvinden in waarschijnlijkheid van een aardbeving met magnitude 7 of hoger naarmate de tijd verstrijkt:
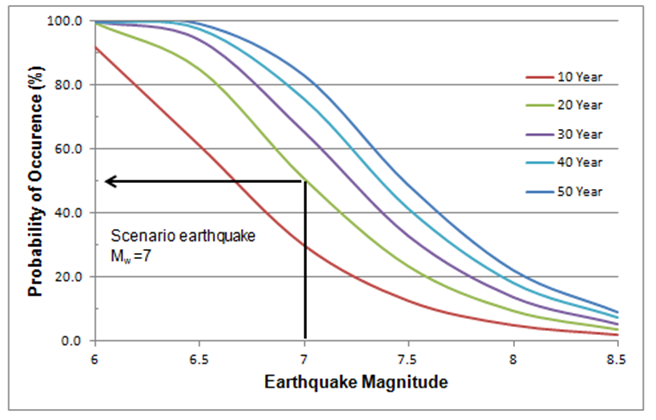
Afbeelding 1
Waarschijnlijkheidsverschuiving van een aardbeving met M ≥ 7
In hoeverre de formule overeenkomt met de werkelijkheid en aardbevingen over het algemeen kan voorspellen, is niet te zeggen. Wel geeft deze formule vrij nauwkeurige benaderingen over de waarschijnlijkheid voor de terugkeer van een aardbeving, wat vooral
van toepassing kan zijn op plekken waar er veel aardbevingen komen.
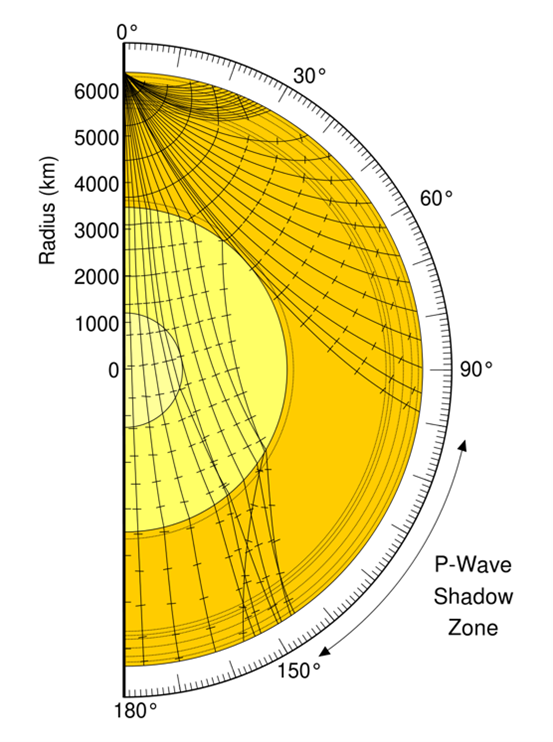
Schaduwzones
Zowel P-golven als S-golven hebben schaduwzones. Dit zijn zones van het aardoppervlak waar een seismische golf nooit aankomt. Omdat een S-golf bijvoorbeeld niet door de vloeibare buitenkern van de aarde kan bewegen, vormt dit gedeelte een schaduwzone
voor de S-golf. Bij de P-golven ligt de schaduwzone tussen de buitenkern en de aardmantel. De schaduwzone bij de P-golven wordt enerzijds veroorzaakt doordat ze seismische-discontinuïteiten meemaken die er weer voor zorgen dat de P-golven
worden afgebroken wanneer ze in een ander medium van de aarde terechtkomen. Bij P-golven gebeurt dit in de buitenkern van de aarde, waar ze als gevolg van de afbreking een lagere snelheid krijgen. Dit verschijnsel is te verklaren met
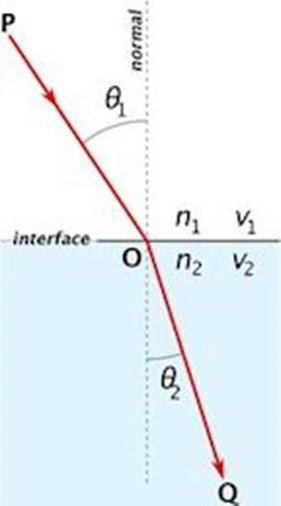
behulp van de wet van Snellius. De wet van Snellius berust op het idee dat de richting en de snelheid van een golf (normaal gesproken licht) verandert, zodra het in een ander medium terechtkomt. Deze wet wordt beschreven volgens:
sin (θ1)
sin (θ2)
=
v1
v2
=
n1
n2
In deze formule zijn θ1 en θ2 de hoeken die de P-golf maakt met de horizontale (lood)lijn op de grens tussen de twee verschillende media: vast gesteente of vloeibare lagen (in rad), v1 en v2 de snelheid van de P-golf vóór en na de refractie (in ms-1), n1 de brekingsindex van het eerste medium en n2 de brekingsindex van het tweede medium.
De brekingsindex is een materiaaleigenschap die iets zegt over de mate waarin het medium een aankomende golf kan vertragen. Er geldt dus: hoe groter de brekingsindex van een bepaald medium is, des te sterker zullende golven in dit medium vertragen. De
wet laat zien dat de P-golven bij het passeren van het ene medium naar het andere medium buigen naar een andere hoek. Hierbij verandert de golfsnelheid van de P-golven en veranderen de brekingsindices zodanig, dat de verhouding tussen
de hoeken, snelheden en brekingsindices constant zijn.
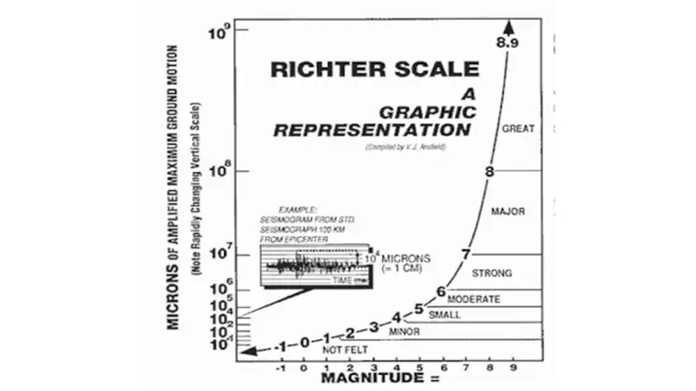
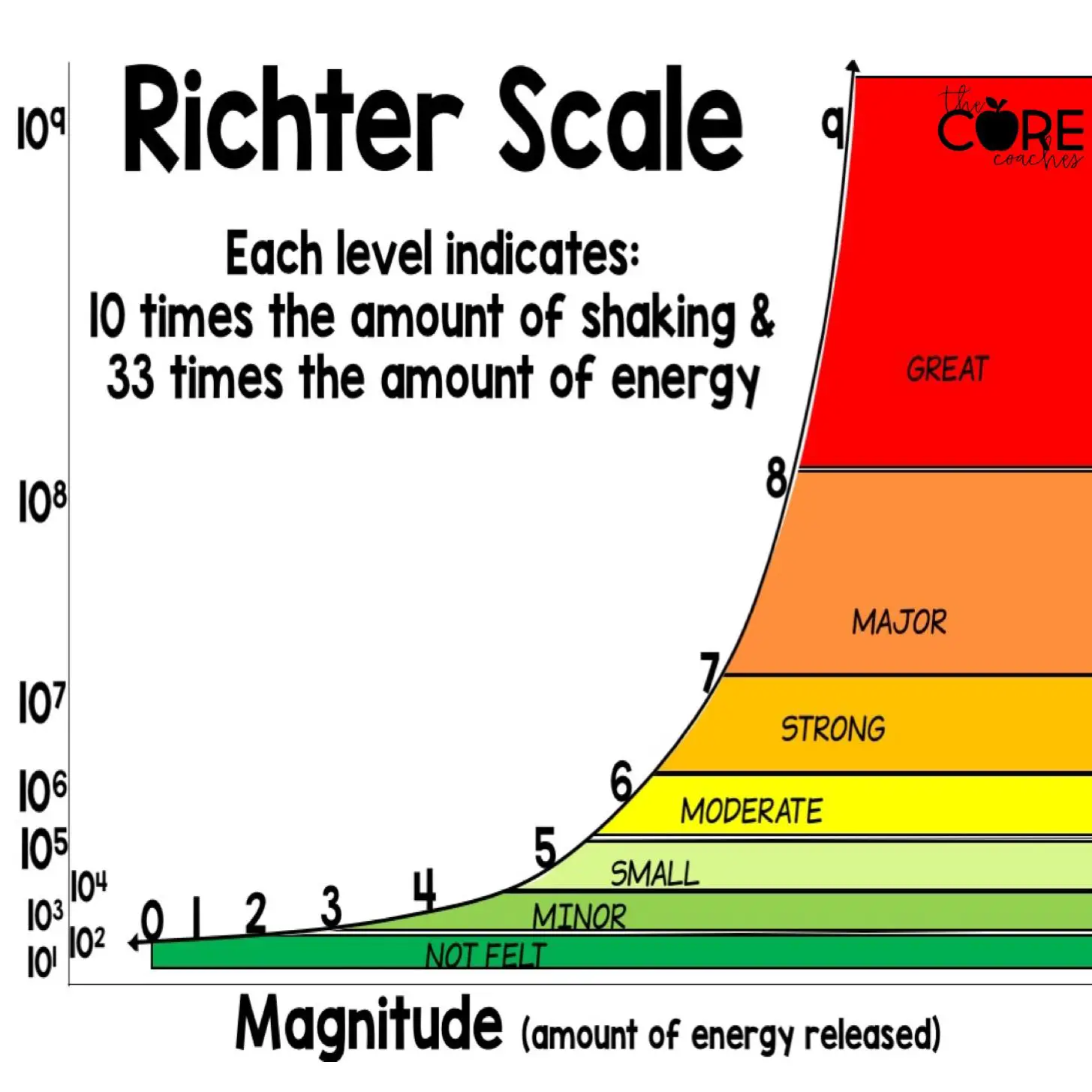
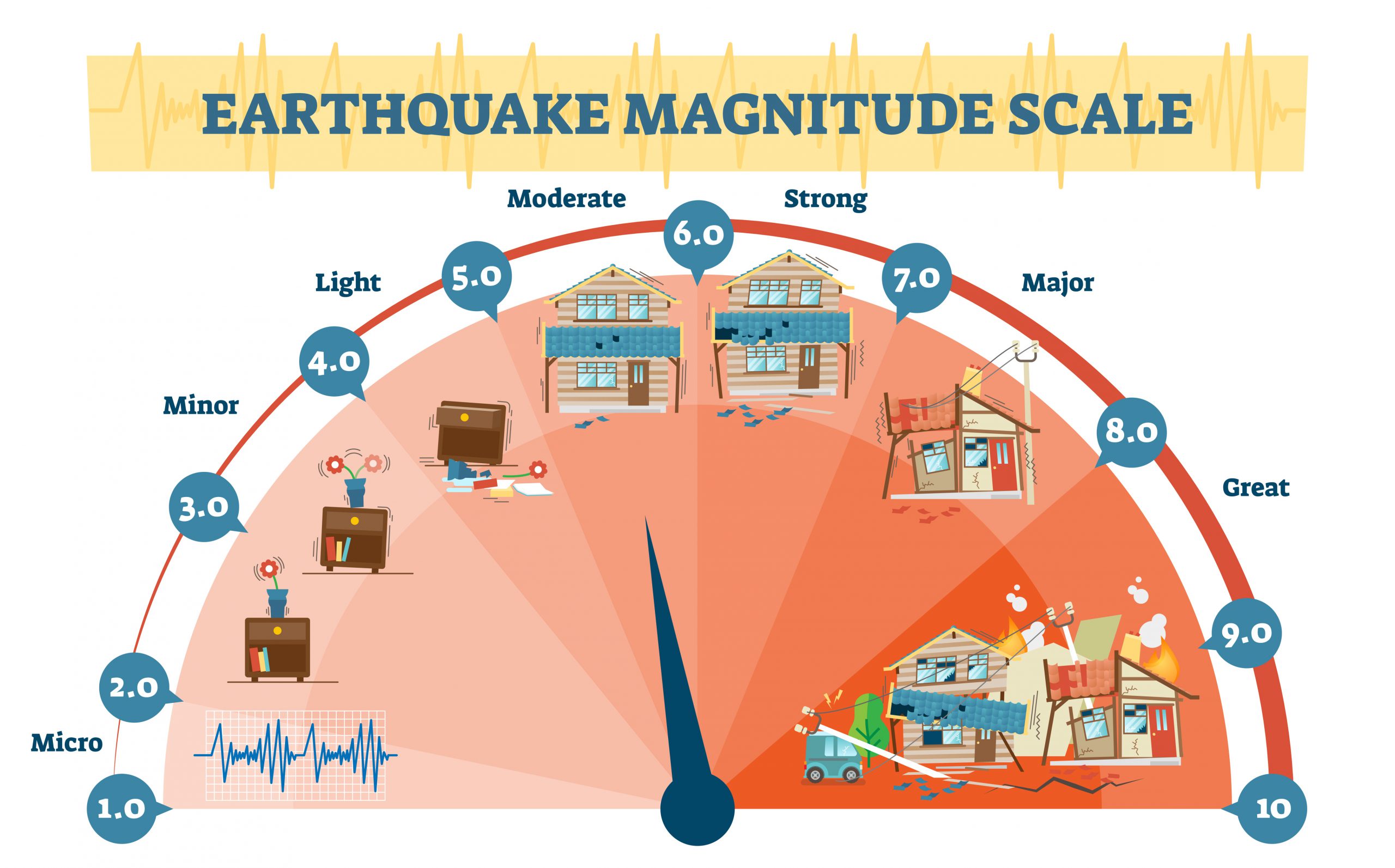
De schaal van Richter
De schaal van Richter, opgericht door Charles F.Richter, speelt een belangrijke rol bij het classificeren van aardbevingen op basis van hun sterktes. Onder de sterkte van een aardbeving wordt de hoeveelheid energie verstaan die vrijkomt bij een beving,
deze wordt ook wel de magnitude (M) van een aardbeving genoemd. De schaal is gebaseerd op de grootte van de amplitudes van de seismische golven die vrijkomen bij de beving. Over het algemeen geldt:
- Aardbevingen met een magnitude van 1,0 tot 3,0 zijn hele kleine aardbevingen en worden nauwelijks gevoeld. Ook veroorzaken ze nauwelijks tot geen schade.
- Aardbevingen met een magnitude tussen 3,0 en 6,0 worden gezien als gematigde aardbevingen. Vaak worden deze gevoeld door de mensen en veroorzaken soms milde schade aan infrastructuur.
- Aardbevingen met een magnitude tussen 6,0 en 7,0 worden beschouwd als sterke aardbevingen. Deze aardbevingen veroorzaken in de meeste schade aanzienlijke schade aan infrastructuur en aan mensen.
- Aardbevingen met een magnitude van 7,0 en hoger zijn zeer schadelijk en worden zelfs als verwoestend beschouwd. Deze aardbevingen zijn dodelijk en kunnen hele gebouwen verwoesten.
De schaal van Richter werkt volgens een logaritmische schaal, waarbij er referentiewaarden3 worden gebruikt. De formule wordt beschreven via een formule die het verband tussen de magnitude en de vrijgekomen
energie door de seismische golven. Omdat deze formule een benadering is, is het vaak niet mogelijk om exact te weten wat de magnitude van een aardbeving is. Dit komt omdat er tegenwoordig met de seismografische apparatuur alleen boven
het aardoppervlak gemeten kan worden. De formule kan worden afgeleid uit een aantal aannames die gelden voor de energie en de amplitude van de seismische golven:
Het verband tussen de energie E en de amplitude A van een aardbeving is evenredig, dus geldt er:
Het verband tussen de energie E en de amplitude A van een aardbeving is evenredig, dus geldt er:
E ~ A
Hieruit kan er een algemene evenredige standaardformule afgeleid worden afgeleid:
E = k × A
Met k als constante. Omdat de schaal van Richter een logaritmische schaal is, moeten beide kanten van de formule worden geschreven in logaritmische vorm. Je krijgt:
log(E) = log(k ∙ A)
Met het feit dat de schaal een referentieschaal is, kan het volgende worden afgeleid:
log(E0) = log(k ∙ A0)
Omdat er geldt: ∆E = k ∙ ∆A kan de formule nu worden samengesteld tot:
log(E) - log(E0) = log(k ∙ A) - log(k ∙ A0)
Het energieverschil zegt iets over de vrijgekomen hoeveelheid energie door de seismische golven tijdens de aardbeving, ofwel ∆E = M en dit geeft:
M = log(k ∙ A) - log(k ∙ A0)
M = log(
)4
k ∙ A
k ∙ A0
M = log(
)
A
A0
Deze formule geeft een benadering voor het verband tussen de magnitude en de amplitude van de seismische golven bij de aardbeving. Omdat deze schaal logaritmisch is, geldt dat de toename van 1 in magnitude (bijv. van 6,0 naar 7,0) resulteert in een aardbeving
die 10 keer zo sterk is.
1 : (researchgate.net, 2006)
2 : (researchgate.net, 2006)
3 : Mathematische waarden die berusten op een verschil ten opzichte van de nulwaarde. Bijvoorbeeld snelheid: v en v0
2 : (researchgate.net, 2006)
3 : Mathematische waarden die berusten op een verschil ten opzichte van de nulwaarde. Bijvoorbeeld snelheid: v en v0
4 : Regel voor logaritmen: log(a) - log(b) = log (
)
a
b